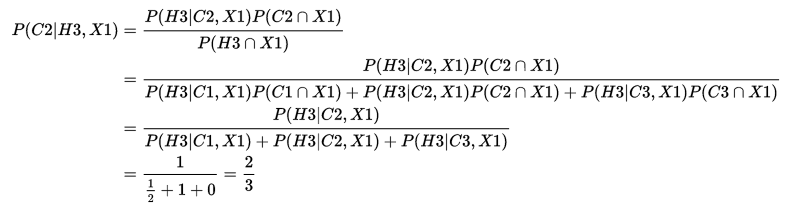Are You Smarter Than a Pigeon?
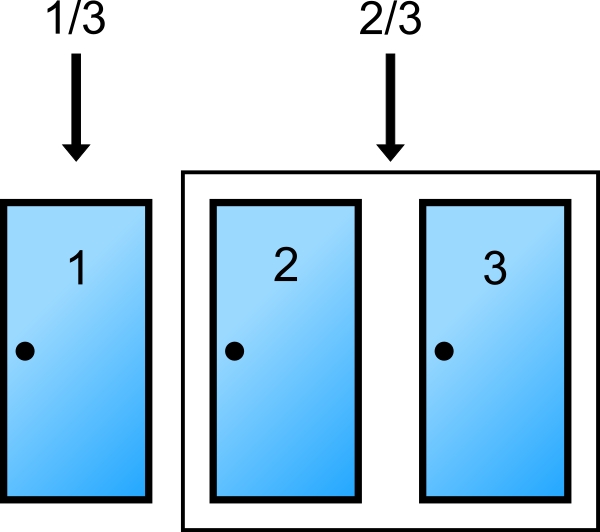
Imagine that you are a contestant on a game show. You are standing in front of three identical doors. Behind one of the doors is a new car. Behind the other two doors are goats.
“Which door do you choose?” Tough decision. Each door has an equal one in three chance of winning you a car. You make your choice:
“I pick Door Number One.”
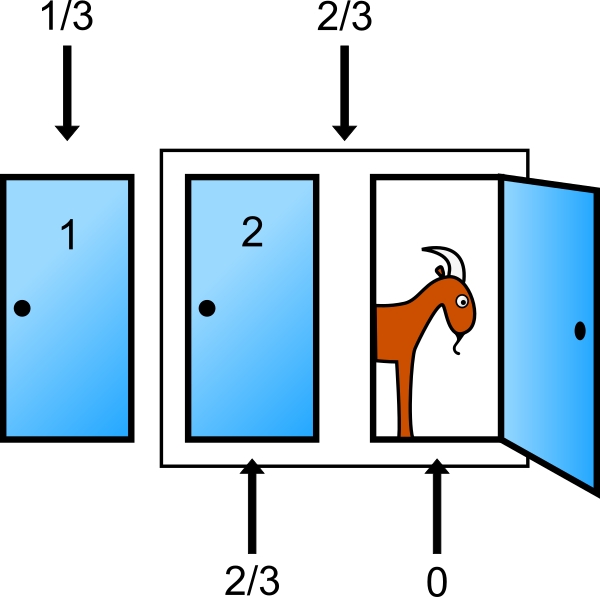
The game show host turns to face the three doors. He asks to have Door Number Three opened. There is a goat. You have watched the show before and know that he always shows the remaining door with a goat.
“Now, you can stay with Door Number One, OR you can switch your choice to Door Number Two! What will it be?”
Should you switch or should you stay? Does it even matter?
Think about your answer. Now, what most people say here is that it doesn’t matter. You are just as likely to win the car if you stay or if you switch. You have a 50/50 chance…
…but that is wrong.
If you switch to Door Number Two, you are twice as likely to win the car than if you stay with Door Number One.
WHAT?!
At this point your face has scrunched up and you are confused. Most people actually become angry and start yelling at me. Please, go ahead and vent for a little bit by yelling at the computer screen about how wrong and stupid I am.
I’ll wait…
Are you done? Oh, sorry. I can wait a little longer…
What you have just been exposed to is what is known as “The Monty Hall Paradox” (Monty Hall was the game show host of Let’s Make a Deal which would present this exact situation to contestants). It is known as one of the most counter-intuitive statistical paradoxes for humans to accept or understand. From time to time the paradox was presented as a riddle in newspapers (Remember those?) and would result in angry letters swearing that it wasn’t true. And not just from every day schmoes like you and me. PhDs, Nobel Laureates, and all kinds of other Certified Smart People (CSPs) have expressed their disagreement (not anymore).
But it’s true.
And it turns out that pigeons learn how it works relatively quickly while most humans just can’t accept it (that article is open access if you care to indulge). Let’s see how you do! (I’ll try to explain it in a couple different ways so if one doesn’t make sense to you, keep reading.)
Base probability
The way the Monty Hall Paradox works is that you must rely on the probability of the base situation. When you first looked at the doors, each door had an equal chance of hiding the car – one in three (1/3). Once you make a choice (Door Number One) something changes slightly. The probability that the car is behind Door Number One is still one in three, but the probability that it is behind EITHER Door Number Two or Door Number Three is two in three (2/3). So Doors Two and Three have a COMBINED probability of 2/3. Unfortunately, you don’t have the option of picking the side with a 2/3 probability…yet.
When the game show host reveals that Door Number Three has a goat behind it, that does not change the base probability of 1/3 vs 2/3. Showing the goat changes nothing about the probability, you always knew there was a goat behind one of those doors. When the game show host asks you if you want to switch from your original choice to the other remaining door, he is asking if you want to change from the group (of one door) with a 1/3 probability to the group (of two doors – one is known to have a goat) with a 2/3 probability. Easy decision since 2/3 are better odds than 1/3: Make the switch.
Oh my. You’re still mad aren’t you? Go ahead and vent again. I know, I’m wrong and that doesn’t make sense. Are you done? You are a cranky one aren’t you?
Switch to the likely group
Another way to look at this is that the game show host actually showed you ALL the doors that absolutely do not have the car behind them, and two remaining doors that are uncertain.
I KNOW!!! SO 50/50 CHANCE BETWEEN THEM! YOU IDIOT!!!
No. Scaling this up would help. Also stop yelling at me.
If there were instead 1,000 doors and you picked one, that would leave 999 doors in the other set (1/1000 vs 999/1000). Now if the game show host opened 998 of those doors to show you 998 goats, leaving you with only two remaining doors (the one you picked and one door from the other 999) would you switch? You’re damn right you would!!! You are picking the one with much greater odds – by far!
Brute force proof
Alright, you’re still skeptical. Showing the brute force breakdown usually works at this point. So here is the table of the possibilities and the outcomes of staying or switching:
There it is again, 1/3 vs 2/3. Trust me, the math works out. If you want to see the math behind the probability of winning by switching to Door Number Two, you can plug it into Bayes’ theorem which looks like this:
Yeah, I don’t understand any of that either. As I mentioned in another post, Bayes’ probability is strongly affected by base rates.
The final proof are the computer simulations. There are many of them out there that have been running for many years. Click through them and see how the probability always falls to 1/3 for staying and 2/3 for switching.
Feel free to yell at them for a while.
The point of all of this is that your intuition of what “makes sense” is really not a very reliable tool by itself.

In summary…
- Game shows are rigged
- Statistics are
also riggeddifficult to understand intuitively - Pigeons can be smarter than people
- Your intuition of what “makes sense” is really not a very reliable tool by itself
The featured image is “Pigeon” by Raghunath Thirumalaisamy via Flickr.
Also included on this post is “MakesSense” by Erik Meira and is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.