Force: Terms and Conditions Apply

I really like that title. With my nerd status, you were probably thinking I would have made some kind of Star Wars reference like “Using the Force” or “The Force Awakens” but Star Wars is actually stupid. I mean, explosion sounds in space? Come on. And how would a light saber even work? I prefer my science fiction hard thank you very much. Also the story is basically just a regurgitation of the monomyth. The only one of those movies I like is Rogue One since it has a healthy dose of nihilism and all of the main characters die in the end (oops, spoilers). I think you underestimated my depth of nerd…
What was I talking about? Oh yeah! Force!
I was asked to write a post that defines the terms around force for sports health and performance professionals. Why? Because teaching that is what I do for a living. I feel that force is the root of those professions, and understanding it allows us to be quantitative (objective) for much longer before we fall into the necessary but sloppy world of the qualitative (subjective). You can think of force as the math around movement. And sadly, in general we don’t understand it as well as we like to think we do.
The terms that we will explore in this post are position, velocity, and acceleration. This will lead us to the terms force, torque, momentum, and impulse and the units that describe them like newtons, newton-meters, and newton-seconds. This is a lot to take on in one post so I will try to keep things simple. There is a whole world (literally) that builds form this. There is math involved – it is the reason we have calculus – but we will avoid most of that for now. We are also going to avoid getting into the terminology weeds of things like velocity vs speed and moment vs torque.
And before we get started, let’s get the citations for this post out of the way…
- Newton, Isaac. Philosophiæ Naturalis Principia Mathematica. London: Edmund Halley; 1687 Jul 5.
That’s it. That’s the citation. It all comes from that (although admittedly Wikipedia is easier to read on the subject).
Derivatives!
Position (location in space), velocity, and acceleration are terms that you are intuitively familiar with already. The three terms are related. In technical terms, velocity is the derivative of position and acceleration is the derivative of velocity (or the second derivative of position). The term derivative refers to instantaneous rate of change. So velocity could be defined as the rate you are changing position, or, how fast you are changing position. That means that acceleration is the rate of change of velocity (or if you want to get meta, the rate of change of the rate of change of position). This should make intuitive sense to you, even if it seems a bit wordy.
Is there a third derivative of position? In other words, a rate of change of acceleration? Absolutely! That’s jerk. And it goes on to forth, fifth, sixth, seventh, etc (jounce, snap, crackle, pop if you are following along at home). But let’s not get over our skis here. To discuss force, we only need to get to the level of acceleration, so we will leave it at that.
Force!
Defining force can get abstract and complicated pretty fast. Technically it is not a “thing” but rather an interaction between two objects (things with mass). It is not something that we really understand intuitively as much as we would think. For example, since it is not a thing, force can’t be “absorbed”. That said, I’m going to let you keep thinking of it that way. Weirdly, for a post about force, it is the one thing I’m not really going to define directly here other than Newton’s famous equation: Force equals mass times acceleration or
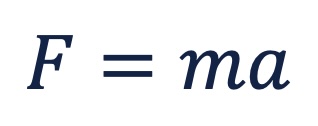
I will provide the definition of its unit of measure, the newton. One newton is the force that accelerates one kilogram of mass one meter per second squared or

Sorry. That’s a Fig Newton. I haven’t eaten yet this morning so I’ve got food on the brain. Let’s try that again. One newton is the amount of force that accelerates one kilogram of mass one meter per second squared or
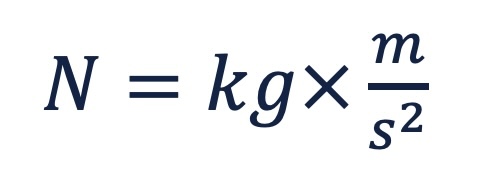
That may look intimidating, but it is just mass (kilogram) times acceleration (meters per second square). Let’s use a thought experiment to understand all of this.
Imagine that I am holding a one kilogram weight straight out from my body. Gravity (I’m not going to define that) is trying to accelerate that weight 9.8 meters per second squared towards the ground, but I am not letting it move. That interaction between my hand and the weight results in 9.8N of force (one kilogram times 9.8 meters per second squared) at my hand.
Torque is rotational force at an axis. That can be calculated by multiplying a force from its distance from the axis it is interacting with. So in the case above, if my arm is 0.7 meters long, the torque at my shoulder (measured in newton-meters) is 6.86Nm (9.8 newtons times 0.7 meters). Here is a professional drawing of all of the math described above
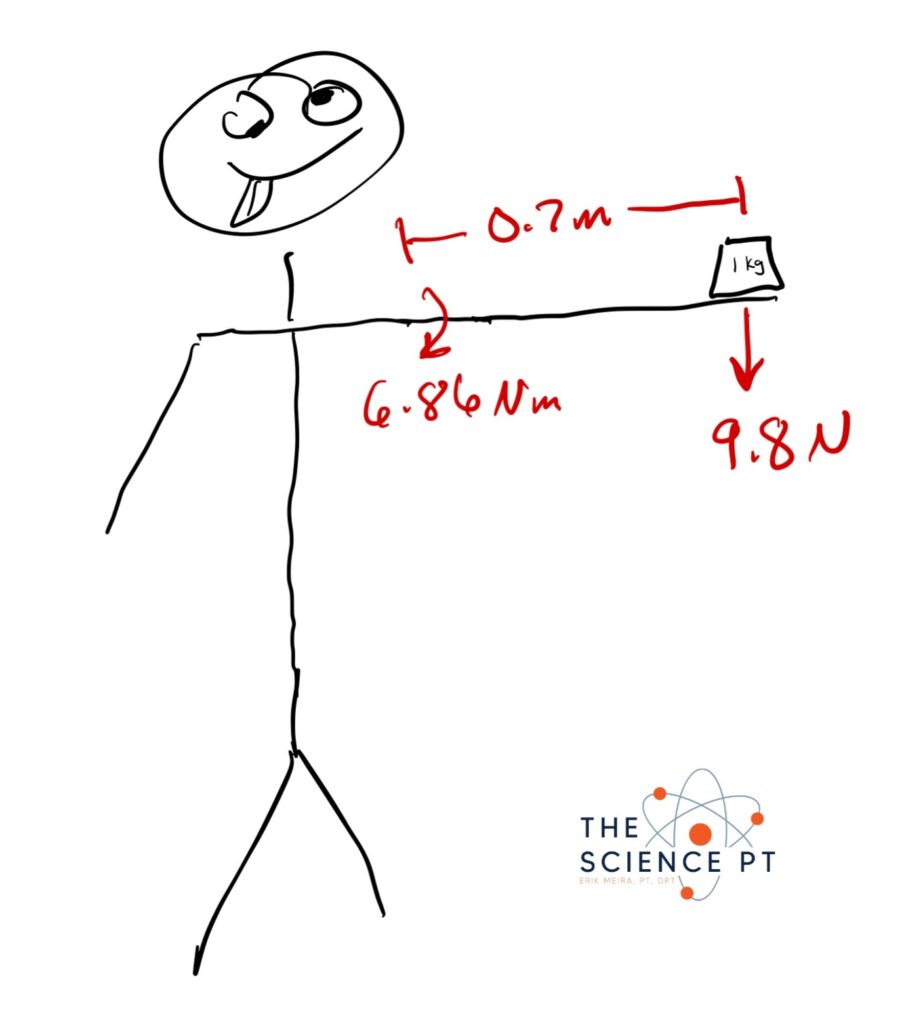
Now let’s go ahead and put torque up on the shelf and not talk about it anymore. It adds a layer of complexity that we don’t need as we go forward. Once you understand these things from the perspective of force, you can apply it to torque later since torque is just rotational force.
Momentum!
At the beginning I described force as the math of movement. So let’s apply all of this to movement!
If something is moving through space, it has mass and it has velocity. You could say that it has momentum since momentum is defined by mass and velocity as per its equation
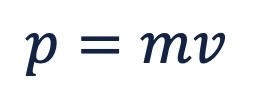
There is a unit for momentum, but for now we are going to leave it at kilograms times meters per second (mass times velocity)
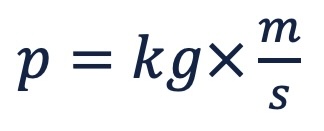
If something has constant momentum, there is no force occurring. But what about if you want to change momentum? Back to a thought experiment!
Imagine that I have a car rolling down the road. My car has mass and it has velocity therefore it has momentum. There is also no expression of force right now if my velocity is constant (let’s forget about road friction, wind resistance, and gravity for now please).
What if someone put a brick wall in front of my car with momentum? I’m probably going to want to change that momentum which means that I need to apply force.
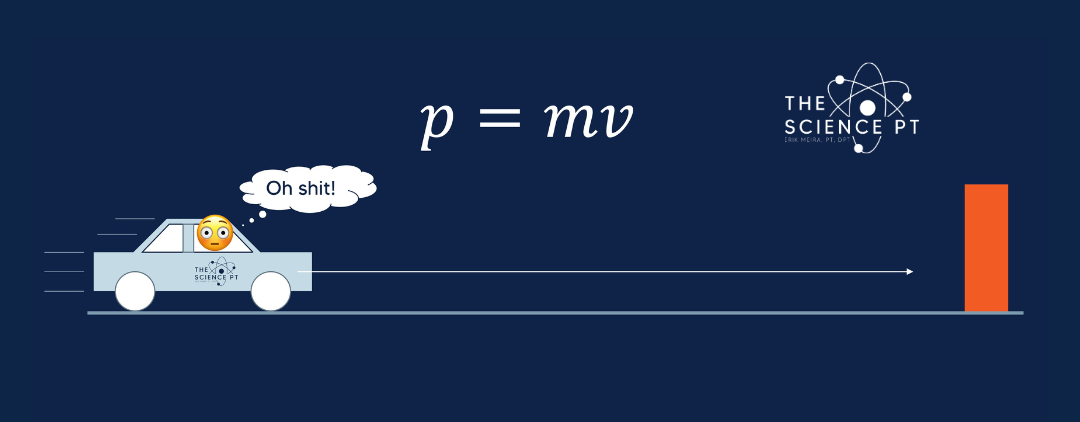
But how much force do I need to apply?
Impulse!
(Why am I using exclamation points on these headings? I’ll stop that on the next one I promise.)
This gets to our final term impulse. And impulse is the most important concept when it comes to our understanding of movement. Impulse is the amount of force and time required to change a certain amount of an object’s momentum. So it is not just force (which is instantaneous) but how long force occurs. Back to the car example.
If I gently applied the brakes (force) for a couple seconds then released them, I changed my momentum a little bit (slowed down). What if I applied those brakes (same force) for longer? Or shorter? That’s a difference in impulse.
The equation for impulse can look scary since it is an integral (the inverse of a derivative).
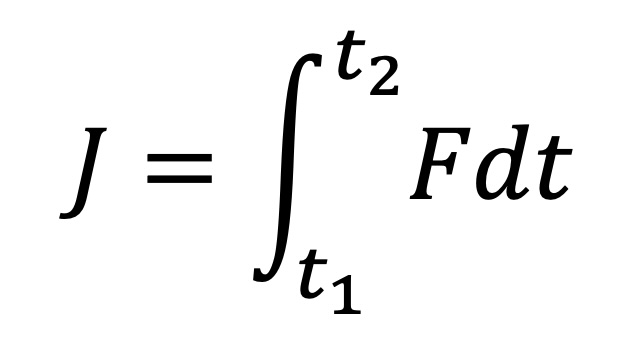
But let’s think of it as I originally described it, force and time. We can say that impulse is force times time which gives us the unit of newton-seconds (Ns). Let’s go back to the car.
If I gently apply the brakes (force) for a long enough time, eventually I will come to a stop (took away all of the momentum). If I were to slam on the brakes (more force), how does that change the time required for stopping? A lot less time.
The key to all of this is that whether I apply the brakes gently or hard, the impulse is the same if I ultimately come to a complete stop. By keeping impulse constant, it creates the inverse relationship between force and time (more force created, less time required; less force created, more time required).
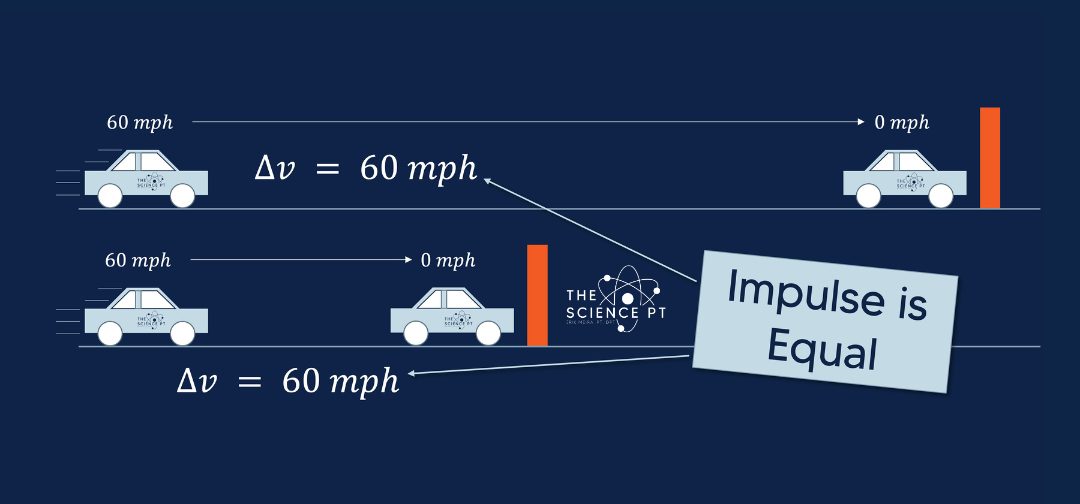
What if I didn’t apply any brakes and just slammed into the wall? Impulse will still be the same since I’ll be coming to a stop. But since I will be achieving that impulse in a very very short amount of time, the force generated will be extremely high (KA-BLAMO! to use a technical term). The shorter the time, the more rate of change required (acceleration), the more rate of change, the more force because F=ma.
In other words, rate matters in momentum change. Because derivatives.
I know what you’re thinking. “Your mother’s a derivative.” Look, insulting someone’s mother is never ok. Mr. T taught me that.
Testing!
(Sorry. Exclamation points are like potato chips. Once you have one, you just can’t stop.)
If I had a car and wanted to test its brakes, I wouldn’t just ask to see if it could stop. Even the worst brakes could stop a car eventually. The fact that a car stops tells you very little about the capacity of its brakes. Until you create a time window (we did this by shortening the distance allowed above).
To me this is like functional testing. Unless you constrain the time required to do the task, you are not assessing performance. An example of this would be something like the 5-0-5 test which creates a time constraint to deceleration into change of direction (as opposed to just looking at ability to change direction). But just like I would test a car brake’s ability to generate impulse BEFORE I would put it in a real-world application, I would test a muscle or joint’s ability to generate impulse before I would do a any kind of related “functional” test, even a great one, like a 5-0-5.
How do you measure impulse? It is looking right at you any time you generate a force-time curve like during an isometric test or force plate measure. It is the area under that curve. (Remember that integral equation from before? Integrals give you areas under curves.)
Here is what it looks like on a five second isometric test (I apologize for using the American ft-lbs or as I like to call them, “Freedom Torque”)
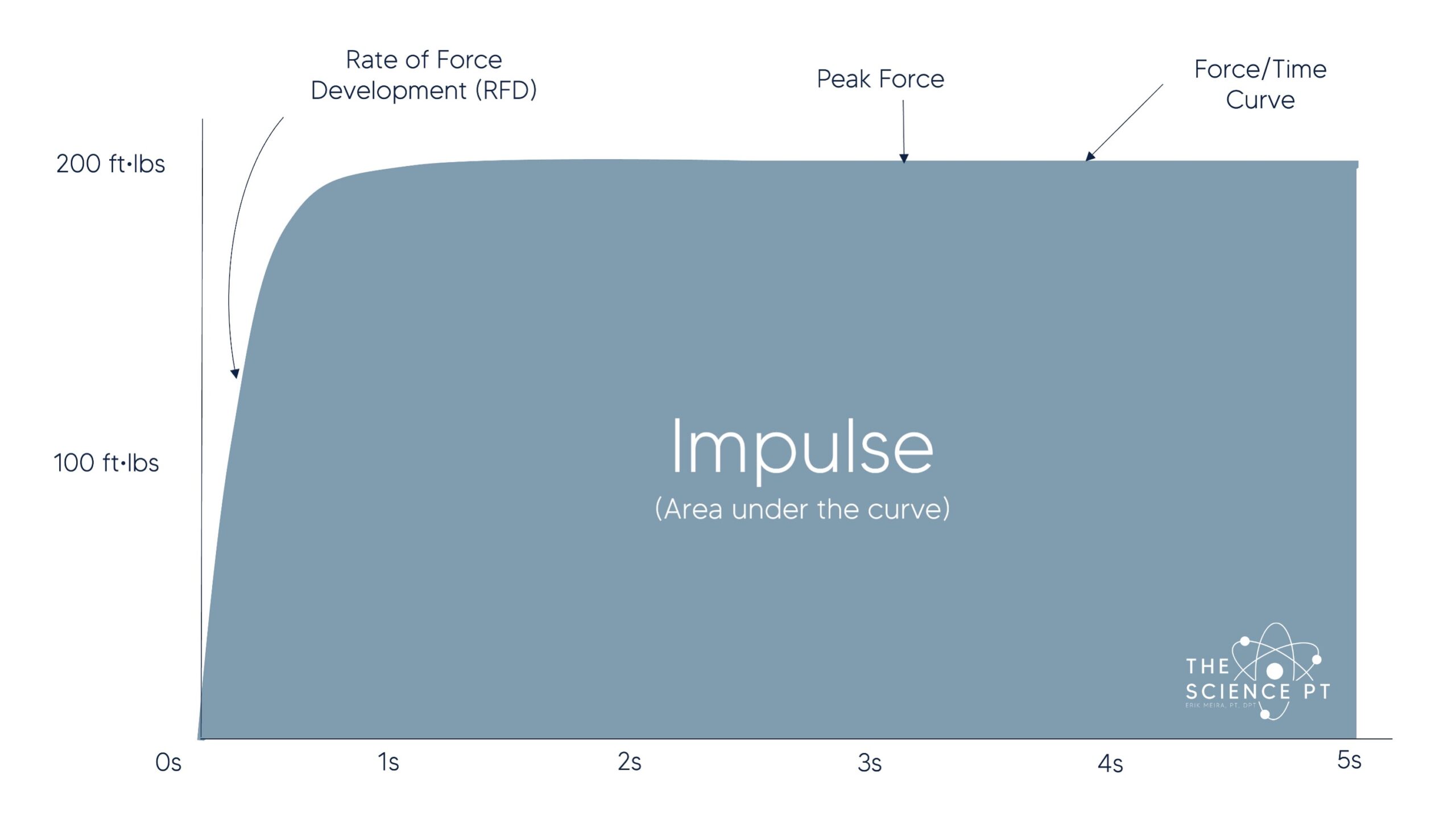
Compare that to this one
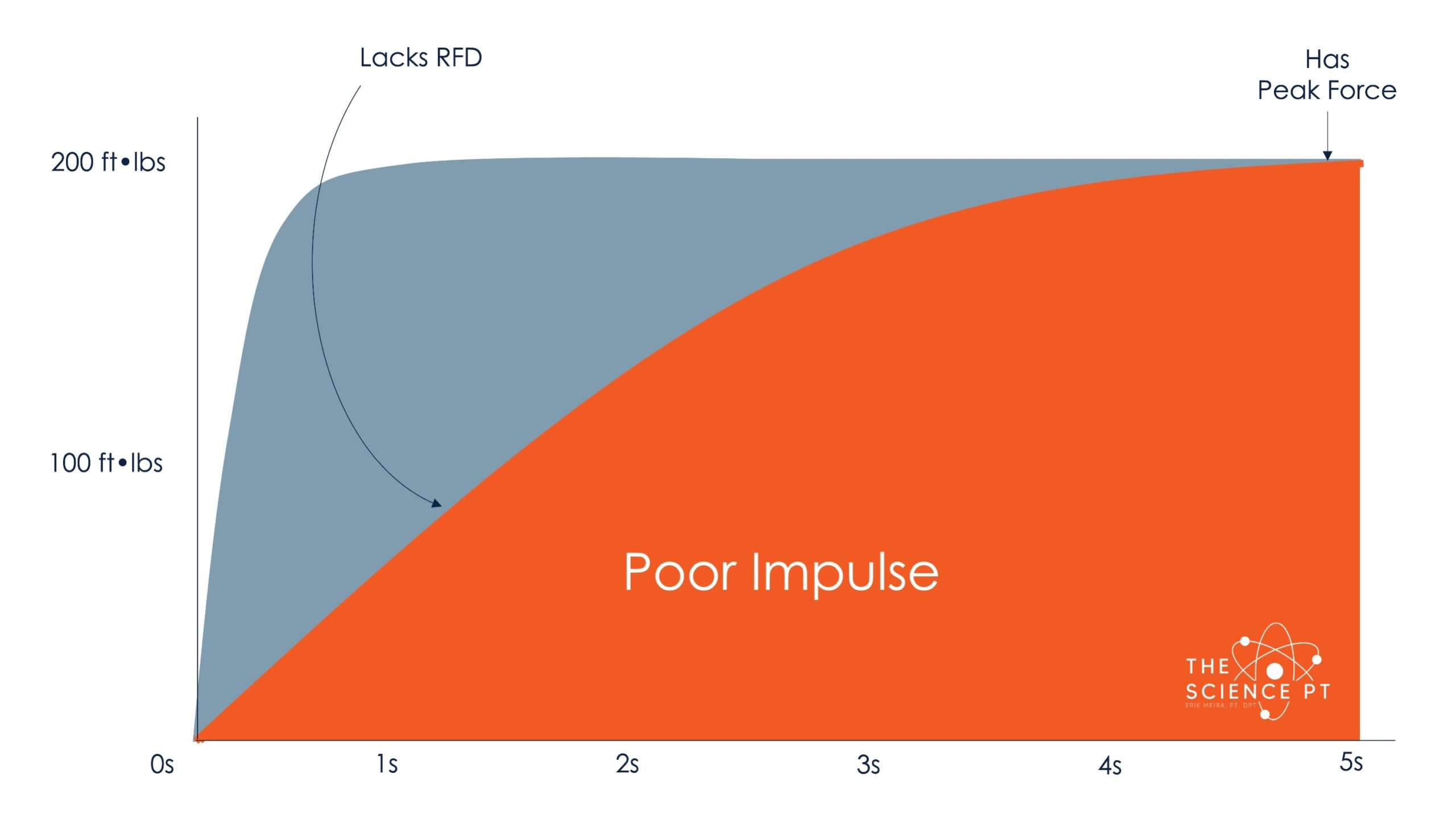
The peak force reached is the same, but impulse achieved is different. In this example, you can see that it is due to a lack of rate. If this person was presented with a task that takes less than 0.5 seconds, there is a huge difference in achievable impulse
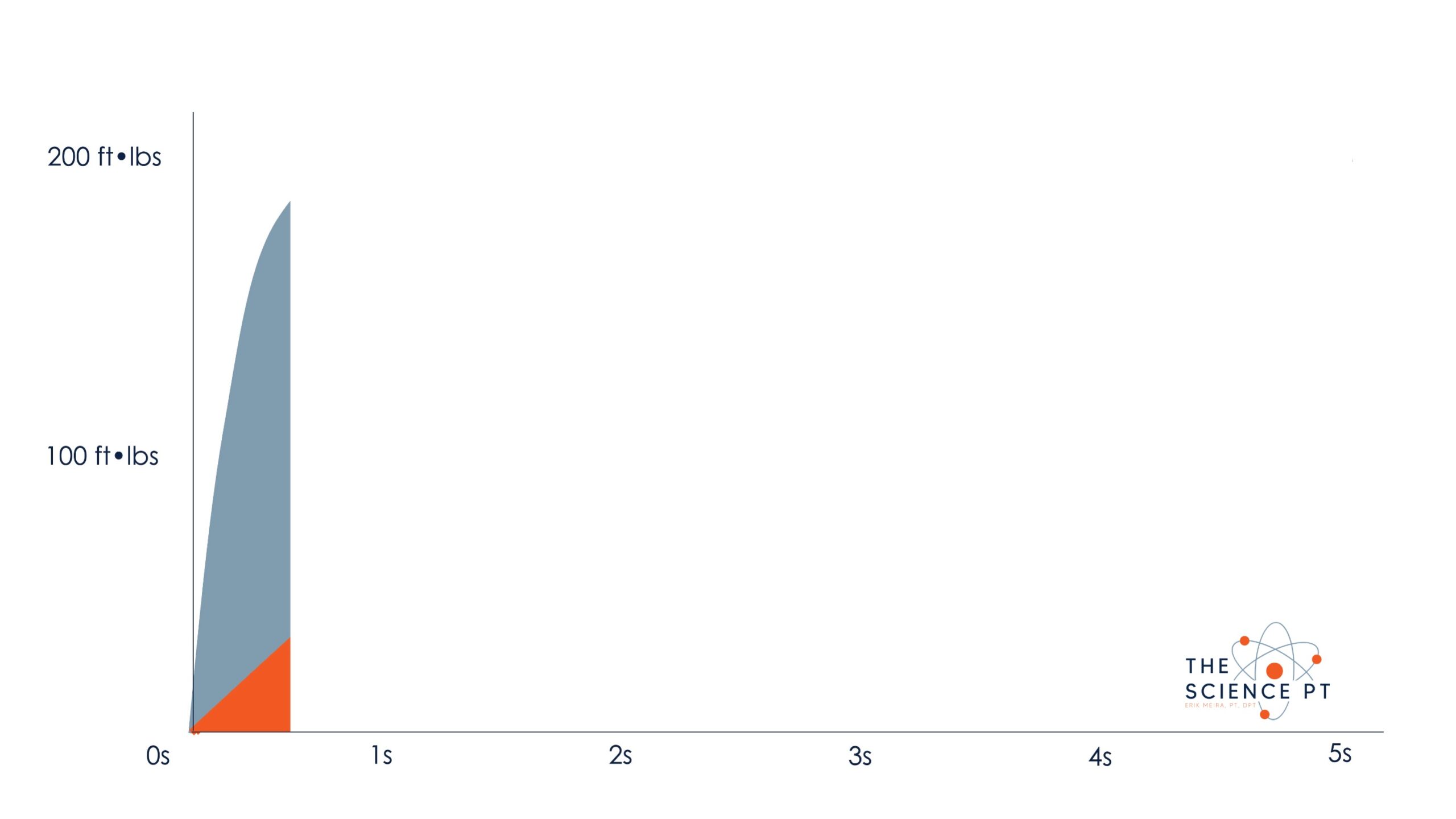
But that doesn’t mean that they couldn’t achieve that impulse at some point. If they took more time, they could reach the same impulse as the other curve
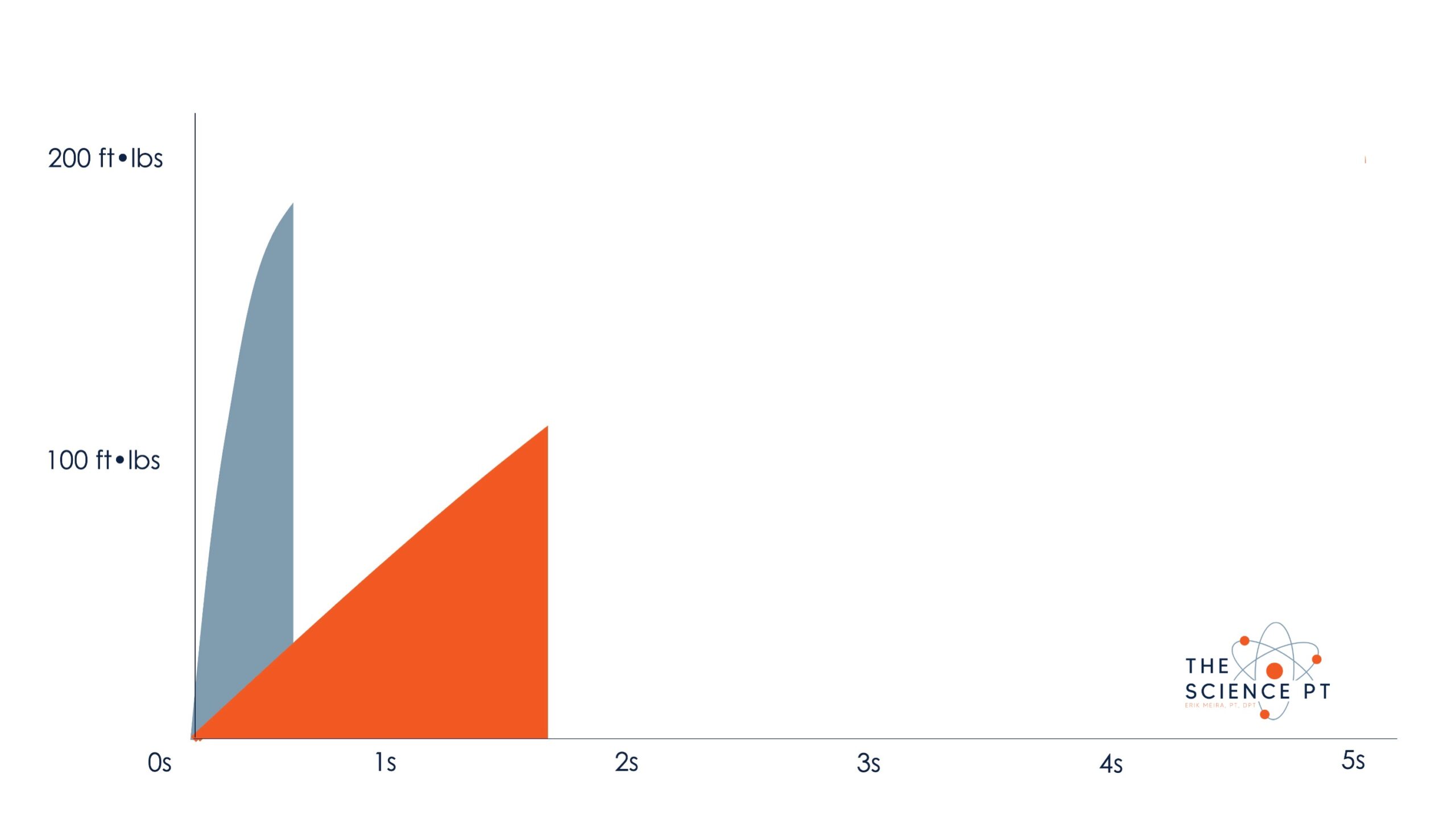
If this was a change or direction for example, everything would look fine except they would have longer ground contact time on the orange side. That’s fine unless you’d like to do it quickly, which, athletes tend to prefer.
I personally think that this is really important to consider during return to play assessments. Just because an athlete can do a task doesn’t mean that they can do the task when constrained by time. By tracking impulse expression, we can anticipate performance difficulties. This allows us to intervene by working on those deficits or knowing that we need to avoid/alter certain real-world load profiles.
In summary…
- Star Wars is stupid
- Rate of change is what defines velocity and acceleration and therefore movement
- Changing momentum requires impulse
- Impulse requires force and time
- We can learn a lot from Mr. T
- By tracking impulse expression, we can anticipate performance difficulties
I teach all of this and a lot more as it applies to knee rehab in my course Complex Understanding for Simple Solutions: The Knee available in person and online.
NOTE: If you were wondering what the unit for momentum is, it is the same as impulse: Newton-seconds. You might be thinking, “But you said to think of it as kilogram times meters per second!” They are the same thing. See the math below…
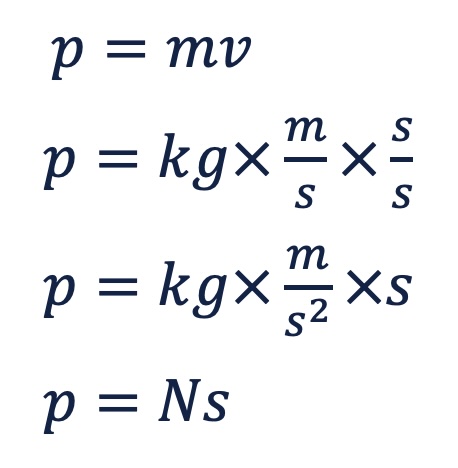
That second over second in the second line is just multiplying by one. That creates kilogram times meters per second squared (which is a newton) times seconds or … newton-seconds. Momentum and impulse use the same units! Isn’t math cool?!
Whatever. Star Wars still sucks.
